Problema de Examen: Dominio y Gráfica de una Función por Tramos
Enunciado del problema
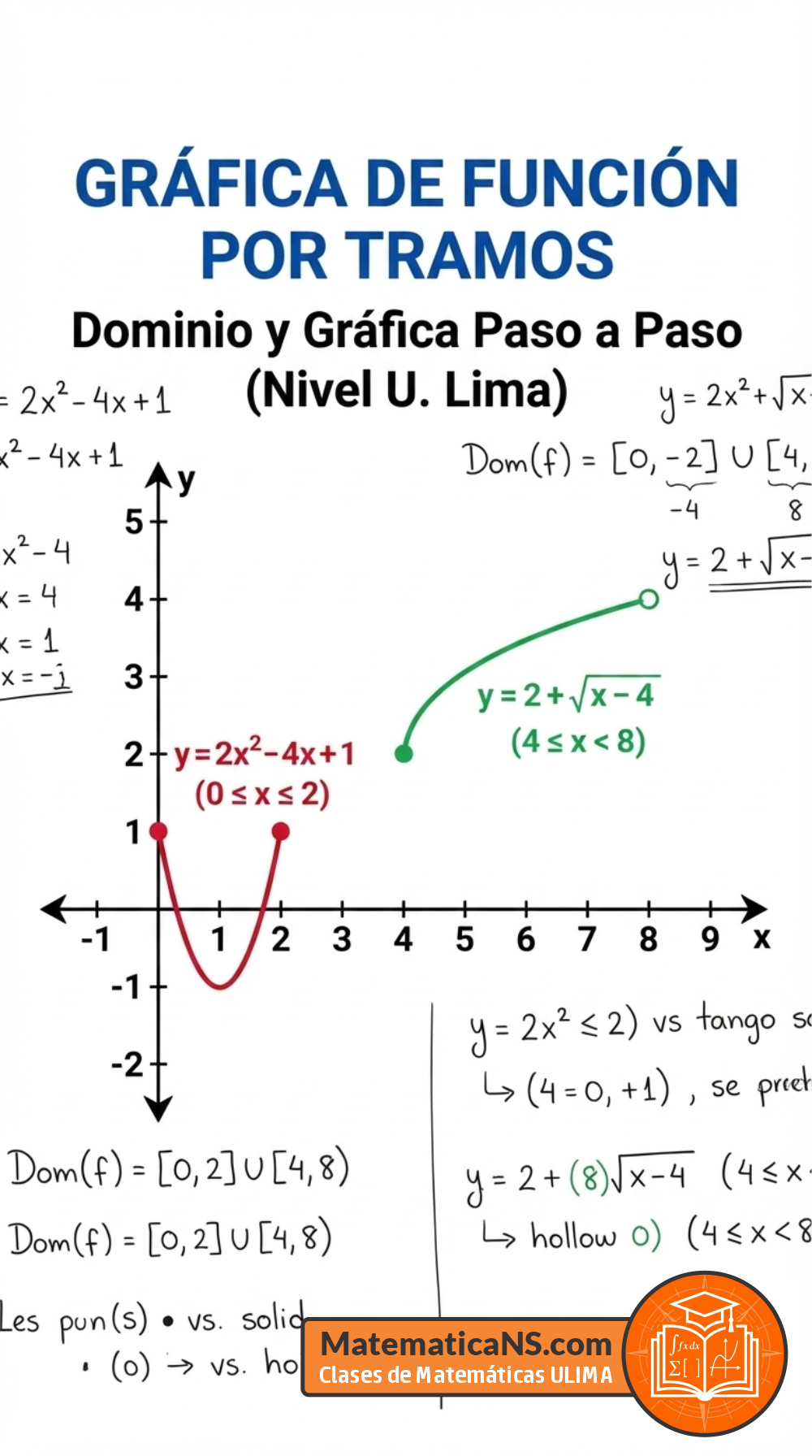
(4P) Halle el dominio y trace la gráfica de la función
$$ f(x) = \begin{cases} 2x^2 – 4x + 1, & 0 \le x \le 2 \\ 2 + \sqrt{x – 4}, & 4 \le x < 8 \end{cases} $$
Teoría necesaria
Una función definida por tramos (o por partes) es aquella que utiliza diferentes fórmulas para distintos intervalos de su dominio. Para trabajar con ellas:
- Dominio: Es la unión de todos los intervalos donde la función está definida.
- Gráfica: Se dibuja la gráfica de cada fórmula únicamente en el intervalo que le corresponde. Es crucial prestar atención a los extremos de los intervalos:
- Usamos un punto cerrado (•) si el extremo está incluido (con \(\le\) o \(\ge\)).
- Usamos un punto abierto o hueco (∘) si el extremo no está incluido (con \(<\) o \(>\)).
Solución detallada
Parte 1: Hallar el Dominio de la Función
El dominio de \(f(x)\) está dado explícitamente por la unión de los intervalos definidos para cada tramo. No hay restricciones adicionales ocultas, ya que la expresión dentro de la raíz cuadrada, \(x-4\), es mayor o igual a cero para todo el intervalo \( [4, 8) \).
- El primer tramo está definido para \( 0 \le x \le 2 \), que corresponde al intervalo \( [0, 2] \).
- El segundo tramo está definido para \( 4 \le x < 8 \), que corresponde al intervalo \( [4, 8) \).
Por lo tanto, el dominio de la función es la unión de estos dos conjuntos:
$$ \text{Dom}(f) = [0, 2] \cup [4, 8) $$
Parte 2: Trazar la Gráfica de la Función
Analizaremos y graficaremos cada tramo por separado en el mismo plano cartesiano.
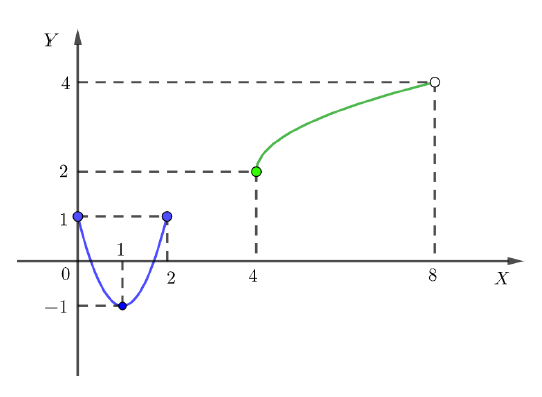
Tramo 1: \( f(x) = 2x^2 – 4x + 1 \) para \( x \in [0, 2] \)
Esta es una función cuadrática, su gráfica es una parábola que se abre hacia arriba (ya que el coeficiente de \(x^2\) es \(2 > 0\)). Para graficarla en el intervalo dado, necesitamos:
- Punto inicial (\(x=0\)):
$$ f(0) = 2(0)^2 – 4(0) + 1 = 1 $$
Como \(x=0\) está incluido (\(\le\)), graficamos un punto cerrado en (0, 1). - Punto final (\(x=2\)):
$$ f(2) = 2(2)^2 – 4(2) + 1 = 8 – 8 + 1 = 1 $$
Como \(x=2\) está incluido (\(\le\)), graficamos un punto cerrado en (2, 1). - Vértice de la parábola: La coordenada x del vértice es \(x_v = \frac{-b}{2a}\).
$$ x_v = \frac{-(-4)}{2(2)} = \frac{4}{4} = 1 $$
El vértice está dentro de nuestro intervalo \([0, 2]\). Hallamos su coordenada y:
$$ y_v = f(1) = 2(1)^2 – 4(1) + 1 = 2 – 4 + 1 = -1 $$
El vértice es el punto (1, -1).
Dibujamos una curva parabólica que va desde (0, 1), baja hasta el vértice (1, -1) y sube hasta (2, 1).
Tramo 2: \( f(x) = 2 + \sqrt{x – 4} \) para \( x \in [4, 8) \)
Esta es una función raíz cuadrada. Su forma base es \(\sqrt{x}\), pero está desplazada 4 unidades a la derecha y 2 unidades hacia arriba. Analizamos los extremos del intervalo:
- Punto inicial (\(x=4\)):
$$ f(4) = 2 + \sqrt{4 – 4} = 2 + \sqrt{0} = 2 $$
Como \(x=4\) está incluido (\(\le\)), graficamos un punto cerrado en (4, 2). - Punto final (\(x \to 8\)): Evaluamos el límite cuando \(x\) se acerca a 8.
$$ f(8) = 2 + \sqrt{8 – 4} = 2 + \sqrt{4} = 2 + 2 = 4 $$
Como \(x=8\) NO está incluido (\(<\)), graficamos un punto abierto (círculo hueco) en (8, 4). - Punto de control: Para ayudar al trazo, podemos elegir un valor intermedio que tenga raíz exacta, por ejemplo \(x=5\).
$$ f(5) = 2 + \sqrt{5 – 4} = 2 + \sqrt{1} = 3 $$
La gráfica pasa por el punto (5, 3).
Dibujamos la curva de la raíz cuadrada partiendo del punto cerrado (4, 2), pasando por (5, 3) y terminando en el punto abierto (8, 4).
La gráfica final consiste en estas dos partes separadas en el plano cartesiano.
Errores comunes
- Confundir puntos abiertos y cerrados: No prestar atención a los símbolos de desigualdad (\(\le, \ge\) vs \(<, >\)) y usar el tipo de punto incorrecto en los extremos de los tramos.
- Graficar fuera del intervalo: Extender la parábola o la curva de la raíz más allá de los límites \( [0, 2] \) y \( [4, 8) \) respectivamente.
- No calcular el vértice de la parábola: Unir simplemente los puntos extremos (0,1) y (2,1) con una línea recta en lugar de una curva que baje hasta el vértice (1, -1).
- Error en el dominio: Intentar unir los intervalos, por ejemplo escribiendo \([0, 8)\), ignorando que la función no está definida entre \(x=2\) y \(x=4\).