Problema de Examen: Análisis y Gráfica de una Función Racional
Enunciado del problema
(5 puntos) Considere la función
$$ f(x) = \frac{x^2}{x^2 – 2x – 3} $$
- Utilice límites para hallar las ecuaciones de las asíntotas horizontales y verticales de \(f\) en caso de que existan.
- Utilice el criterio de la primera derivada para hallar los extremos relativos de la función \(f\) y sus intervalos de crecimiento.
- Con la información obtenida en (a) y (b), grafique \(f\).
Teoría mínima necesaria
Para realizar el análisis completo de una función racional \(f(x) = \frac{P(x)}{Q(x)}\), necesitamos los siguientes conceptos:
- Asíntotas Verticales: Son rectas verticales \(x=c\) donde la función tiende a infinito. Se encuentran en los valores de \(x\) que anulan el denominador (\(Q(c)=0\)) pero no el numerador, y se confirma con \(\lim_{x \to c} f(x) = \pm \infty\).
- Asíntotas Horizontales: Son rectas horizontales \(y=L\) a las que se aproxima la función cuando \(x \to \pm \infty\). Se hallan calculando \(\lim_{x \to \infty} f(x)\) y \(\lim_{x \to -\infty} f(x)\). Si el grado de \(P(x)\) es igual al grado de \(Q(x)\), la asíntota es el cociente de los coeficientes principales.
- Criterio de la Primera Derivada: Sirve para determinar intervalos de crecimiento/decrecimiento y extremos relativos.
- Si \(f'(x) > 0\) en un intervalo, \(f\) es creciente en ese intervalo.
- Si \(f'(x) < 0\) en un intervalo, \(f\) es decreciente.
- Si \(f'(x)\) cambia de signo en un punto crítico \(c\), hay un extremo relativo (máximo si cambia de + a -, mínimo si cambia de – a +).
- Puntos Críticos: Son los valores de \(x\) en el dominio de \(f\) donde \(f'(x) = 0\) o donde \(f'(x)\) no existe.
Solución detallada
Parte (a): Asíntotas Horizontales y Verticales
La función es \(f(x) = \frac{x^2}{x^2 – 2x – 3}\).
1. Asíntotas Verticales (A.V.):
Buscamos donde el denominador es cero: \(x^2 – 2x – 3 = 0\).
Factorizamos el trinomio: \((x – 3)(x + 1) = 0\).
Los candidatos a A.V. son \(x = 3\) y \(x = -1\). Verificamos que no anulen el numerador.
- Para \(x = 3\), numerador es \(3^2 = 9 \neq 0\). Confirmamos con límites laterales: \(\lim_{x \to 3^+} \frac{x^2}{(x-3)(x+1)} = \frac{9}{(0^+)(4)} = +\infty\). Por lo tanto, \(x = 3\) es una A.V.
- Para \(x = -1\), numerador es \((-1)^2 = 1 \neq 0\). Confirmamos con límites laterales: \(\lim_{x \to -1^+} \frac{x^2}{(x-3)(x+1)} = \frac{1}{(-4)(0^+)} = -\infty\). Por lo tanto, \(x = -1\) es una A.V.
2. Asíntotas Horizontales (A.H.):
Calculamos el límite al infinito. Como los grados del numerador y denominador son iguales (ambos son 2), la A.H. es el cociente de los coeficientes principales:
$$ \lim_{x \to \pm \infty} f(x) = \lim_{x \to \pm \infty} \frac{x^2}{x^2 – 2x – 3} = \frac{1}{1} = 1 $$
Por lo tanto, \(y = 1\) es una A.H.
Parte (b): Extremos relativos e intervalos de crecimiento
Usamos el criterio de la primera derivada. Derivamos \(f(x)\) usando la regla del cociente.
Sea \(u = x^2 \implies u’ = 2x\)
Sea \(v = x^2 – 2x – 3 \implies v’ = 2x – 2\)
$$ f'(x) = \frac{u’v – uv’}{v^2} = \frac{(2x)(x^2 – 2x – 3) – (x^2)(2x – 2)}{(x^2 – 2x – 3)^2} $$
Simplificamos el numerador:
Numerador = \( 2x^3 – 4x^2 – 6x – (2x^3 – 2x^2) \)
Numerador = \( 2x^3 – 4x^2 – 6x – 2x^3 + 2x^2 \)
Numerador = \( -2x^2 – 6x \)
Entonces, la derivada es:
$$ f'(x) = \frac{-2x^2 – 6x}{(x^2 – 2x – 3)^2} = \frac{-2x(x + 3)}{(x^2 – 2x – 3)^2} $$
Puntos Críticos:
- Donde \(f'(x) = 0\): Igualamos el numerador a cero.\(-2x(x + 3) = 0\)Esto ocurre si \(x = 0\) o \(x = -3\). Ambos puntos están en el dominio de \(f\).
- Donde \(f'(x)\) no existe: El denominador es cero en \(x = 3\) y \(x = -1\). Estos no son puntos críticos porque no están en el dominio de \(f\), pero son importantes para el análisis de signos.
Análisis de Signos de \(f'(x)\):
Usamos los puntos críticos y las A.V. para dividir la recta numérica en intervalos: \( (-\infty, -3), (-3, -1), (-1, 0), (0, 3), (3, \infty) \). El denominador \((x^2 – 2x – 3)^2\) siempre es positivo, así que el signo de \(f'(x)\) depende solo del numerador \(-2x(x+3)\).
| Intervalo | Punto de prueba | Signo de \(f'(x)\) | Comportamiento de \(f(x)\) |
|---|---|---|---|
| \((-\infty, -3)\) | \(x = -4\) | \(-2(-4)(-4+3) = -8 < 0\) | Decreciente |
| \((-3, -1)\) | \(x = -2\) | \(-2(-2)(-2+3) = +4 > 0\) | Creciente |
| \((-1, 0)\) | \(x = -0.5\) | \(-2(-0.5)(-0.5+3) = +2.5 > 0\) | Creciente |
| \((0, 3)\) | \(x = 1\) | \(-2(1)(1+3) = -8 < 0\) | Decreciente |
| \((3, \infty)\) | \(x = 4\) | \(-2(4)(4+3) = -56 < 0\) | Decreciente |
Conclusiones:
- Intervalos de crecimiento: \((-3, -1) \cup (-1, 0)\).
- Intervalos de decrecimiento: \((-\infty, -3) \cup (0, 3) \cup (3, \infty)\).
- Extremos relativos:
- En \(x = -3\), \(f'(x)\) cambia de negativo a positivo, por lo que hay un Mínimo Relativo.\(f(-3) = \frac{(-3)^2}{(-3)^2 – 2(-3) – 3} = \frac{9}{9 + 6 – 3} = \frac{9}{12} = \frac{3}{4}\). Punto: \((-3, 3/4)\).
- En \(x = 0\), \(f'(x)\) cambia de positivo a negativo, por lo que hay un Máximo Relativo.\(f(0) = \frac{0^2}{0^2 – 2(0) – 3} = \frac{0}{-3} = 0\). Punto: \((0, 0)\).
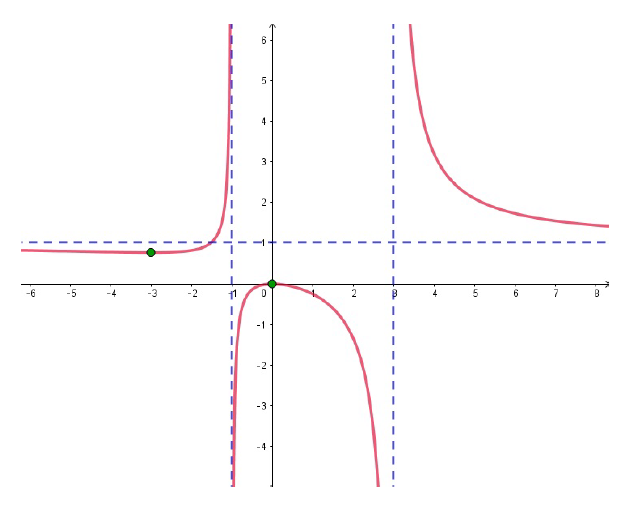
Parte (c): Gráfica de \(f\)
Para graficar, usamos toda la información recopilada:
- Dibujamos las Asíntotas Verticales: líneas discontinuas en \(x = -1\) y \(x = 3\).
- Dibujamos la Asíntota Horizontal: línea discontinua en \(y = 1\).
- Marcamos los Extremos Relativos: el mínimo en \((-3, 0.75)\) y el máximo en \((0, 0)\).
- Usamos los intervalos de crecimiento y decrecimiento para trazar la curva, asegurándonos de que se acerque a las asíntotas de forma correcta.
- A la izquierda de \(x=-3\), la función viene de la A.H. \(y=1\) y decrece hasta el mínimo.
- Entre \(x=-3\) y \(x=-1\), crece desde el mínimo hacia la A.V. \(x=-1\) (tiende a \(+\infty\) si nos acercamos por la izquierda).
- Entre \(x=-1\) y \(x=0\), crece desde la A.V. \(x=-1\) (viene de \(-\infty\)) hasta el máximo en \((0,0)\).
- Entre \(x=0\) y \(x=3\), decrece desde el máximo hacia la A.V. \(x=3\) (tiende a \(-\infty\)).
- A la derecha de \(x=3\), la función viene de la A.V. (tiende a \(+\infty\)) y decrece acercándose a la A.H. \(y=1\).
Errores comunes
- Olvidar verificar el numerador en A.V.: Asumir que todos los ceros del denominador son A.V. sin comprobar si anulan también el numerador (lo que sería un hueco, no una asíntota).
- Error en la Regla del Cociente: Un error muy frecuente al derivar es equivocarse en el signo del numerador: \(u’v \boldsymbol{-} uv’\).
- Ignorar las A.V. en la tabla de signos: No incluir los valores donde el denominador se hace cero (\(x=-1, x=3\)) al dividir la recta numérica para analizar \(f'(x)\), lo que lleva a conclusiones erróneas sobre los intervalos.
- Confundir máximos y mínimos: No aplicar correctamente el criterio del cambio de signo de la derivada para clasificar los extremos.
- Gráfica inconsistente: Trazar una gráfica que cruza una A.V. o que no respeta los intervalos de crecimiento y decrecimiento hallados.





