Problema de Examen: Operaciones con Conjuntos e Intervalos Reales
Enunciado del problema
Pregunta 4 (6 puntos)
Dados los siguientes conjuntos:
$$ A = \{x \in \mathbb{R} / (3x – 4) \in \langle -1; 2x]\} $$
$$ B = \{x \in \mathbb{R} / (4x + 1) \in [9; +\infty)’\} $$
$$ C = [-2; 3\rangle $$
determine:
a) (2P) El intervalo o la unión de intervalos que le corresponde al conjunto A.
b) (2P) El intervalo o la unión de intervalos que le corresponde al conjunto B.
c) (1P) \( (A – B) \cap C \).
d) (1P) \( \mathbb{Z} – C’ \).
Teoría mínima necesaria
Para resolver este problema, necesitamos entender los siguientes conceptos sobre intervalos y operaciones con conjuntos:
- Intervalos: Son subconjuntos de la recta real.
- Abierto \(\langle a; b\rangle\): Números estrictamente entre \(a\) y \(b\) (\(a < x < b\)).
- Cerrado \([a; b]\): Números entre \(a\) y \(b\), incluyendo los extremos (\(a \le x \le b\)).
- Semiabierto (ej. \([a; b\rangle\)): Incluye un extremo pero no el otro (\(a \le x < b\)).
- Operaciones con Conjuntos:
- Intersección (\(A \cap B\)): Elementos que pertenecen simultáneamente a \(A\) y a \(B\).
- Diferencia (\(A – B\)): Elementos que pertenecen a \(A\) pero NO pertenecen a \(B\).
- Complemento (\(A’\)): Todos los elementos del universo (en este caso \(\mathbb{R}\)) que NO pertenecen a \(A\). Es decir, \(A’ = \mathbb{R} – A\).
- Conjunto \(\mathbb{Z}\): Es el conjunto de los números enteros \(\{…, -2, -1, 0, 1, 2, …\}\).
Solución detallada
a) Determinar el conjunto A
La condición es \((3x – 4) \in \langle -1; 2x]\). Esto se traduce en una doble inecuación:
$$ -1 < 3x – 4 \le 2x $$
Separamos esto en dos inecuaciones que deben cumplirse al mismo tiempo (intersección):
- \( -1 < 3x – 4 \)
Sumamos 4 a ambos lados:
\( 3 < 3x \)Dividimos entre 3:
\( 1 < x \implies x \in \langle 1; +\infty\rangle \) - \( 3x – 4 \le 2x \)
Restamos \(2x\) a ambos lados:
\( x – 4 \le 0 \)Sumamos 4 a ambos lados:
\( x \le 4 \implies x \in \langle -\infty; 4] \)
El conjunto A es la intersección de estas dos soluciones:
$$ A = \langle 1; +\infty\rangle \cap \langle -\infty; 4] $$
Visualizando en la recta numérica, la parte común es:
$$ \mathbf{A = \langle 1; 4]} $$
b) Determinar el conjunto B
La condición es \((4x + 1) \in [9; +\infty)’\). Primero, hallamos el complemento del intervalo \([9; +\infty)\).
El complemento son todos los números reales que no están en \([9; +\infty)\), es decir, los números menores que 9.
$$ [9; +\infty)’ = \langle -\infty; 9\rangle $$
Ahora, la condición es \((4x + 1) \in \langle -\infty; 9\rangle\), lo que significa:
$$ 4x + 1 < 9 $$
Resolvemos la inecuación:
Restamos 1: \( 4x < 8 \)
Dividimos entre 4: \( x < 2 \)
Por lo tanto, el intervalo para B es:
$$ \mathbf{B = \langle -\infty; 2\rangle} $$
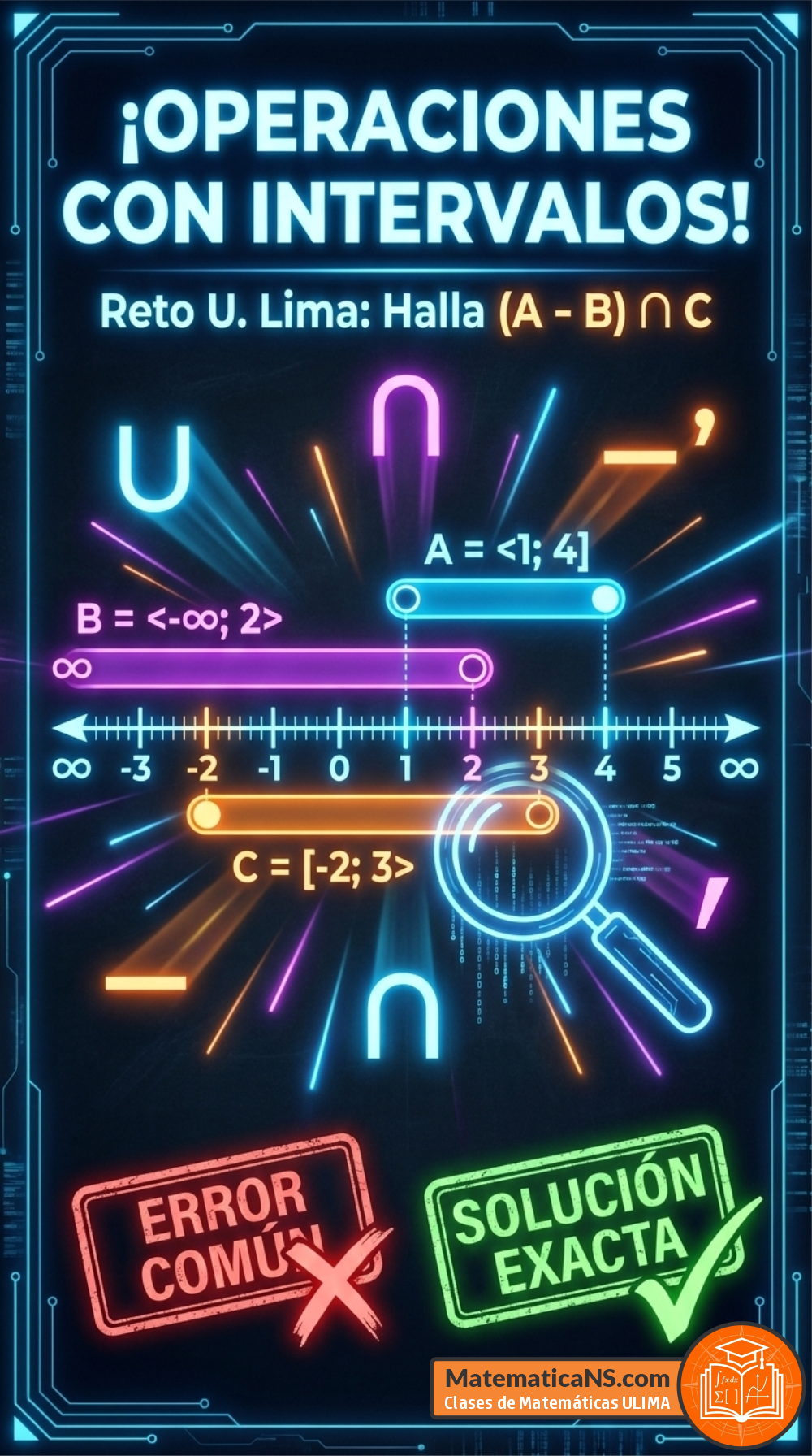
c) Calcular \( (A – B) \cap C \)
Tenemos los conjuntos: \( A = \langle 1; 4] \), \( B = \langle -\infty; 2\rangle \) y \( C = [-2; 3\rangle \).
Paso 1: Hallar \( A – B \)
Buscamos los elementos que están en \(A\) pero no en \(B\).
- \(A\) es el intervalo de 1 (excluido) a 4 (incluido).
- \(B\) son todos los números menores que 2.
Si quitamos de \(A\) todos los números menores que 2, nos quedamos con los números desde 2 (incluido, porque 2 no está en B) hasta 4 (incluido).
$$ A – B = [2; 4] $$
Paso 2: Hallar la intersección con \( C \)
Ahora buscamos la parte común entre \([2; 4]\) y \(C = [-2; 3\rangle\).
- El primer intervalo va de 2 a 4.
- El segundo intervalo va de -2 a casi 3.
La superposición comienza en 2 y termina justo antes de 3.
$$ (A – B) \cap C = [2; 4] \cap [-2; 3\rangle = \mathbf{[2; 3\rangle} $$
d) Calcular \( \mathbb{Z} – C’ \)
Podemos simplificar esta expresión usando propiedades de conjuntos. La diferencia \(X – Y\) es lo mismo que \(X \cap Y’\). Entonces:
$$ \mathbb{Z} – C’ = \mathbb{Z} \cap (C’)’ $$
El complemento del complemento de un conjunto es el conjunto original (\((C’)’ = C\)). Así que la operación se reduce a:
$$ \mathbb{Z} – C’ = \mathbb{Z} \cap C $$
Esto significa que debemos encontrar los **números enteros** que pertenecen al intervalo \( C = [-2; 3\rangle \).
El intervalo incluye al -2 y llega hasta antes del 3. Los enteros en este rango son:
$$ \mathbf{\{-2, -1, 0, 1, 2\}} $$
Errores comunes
- Mal manejo de inecuaciones dobles: No separar correctamente la doble inecuación en dos partes y luego interceptar las soluciones.
- Confusión con los extremos: Usar corchetes \([]\) cuando deberían ser \(\langle\rangle\) o viceversa, especialmente al hallar complementos o diferencias.
- Error al restar intervalos: En \(A – B\), no identificar correctamente qué parte del intervalo \(A\) se «corta» por \(B\). Ayuda mucho dibujar la recta numérica.
- Olvidar qué es \(\mathbb{Z}\): No recordar que se buscan solo números enteros en la parte d) y dar un intervalo como respuesta en su lugar.