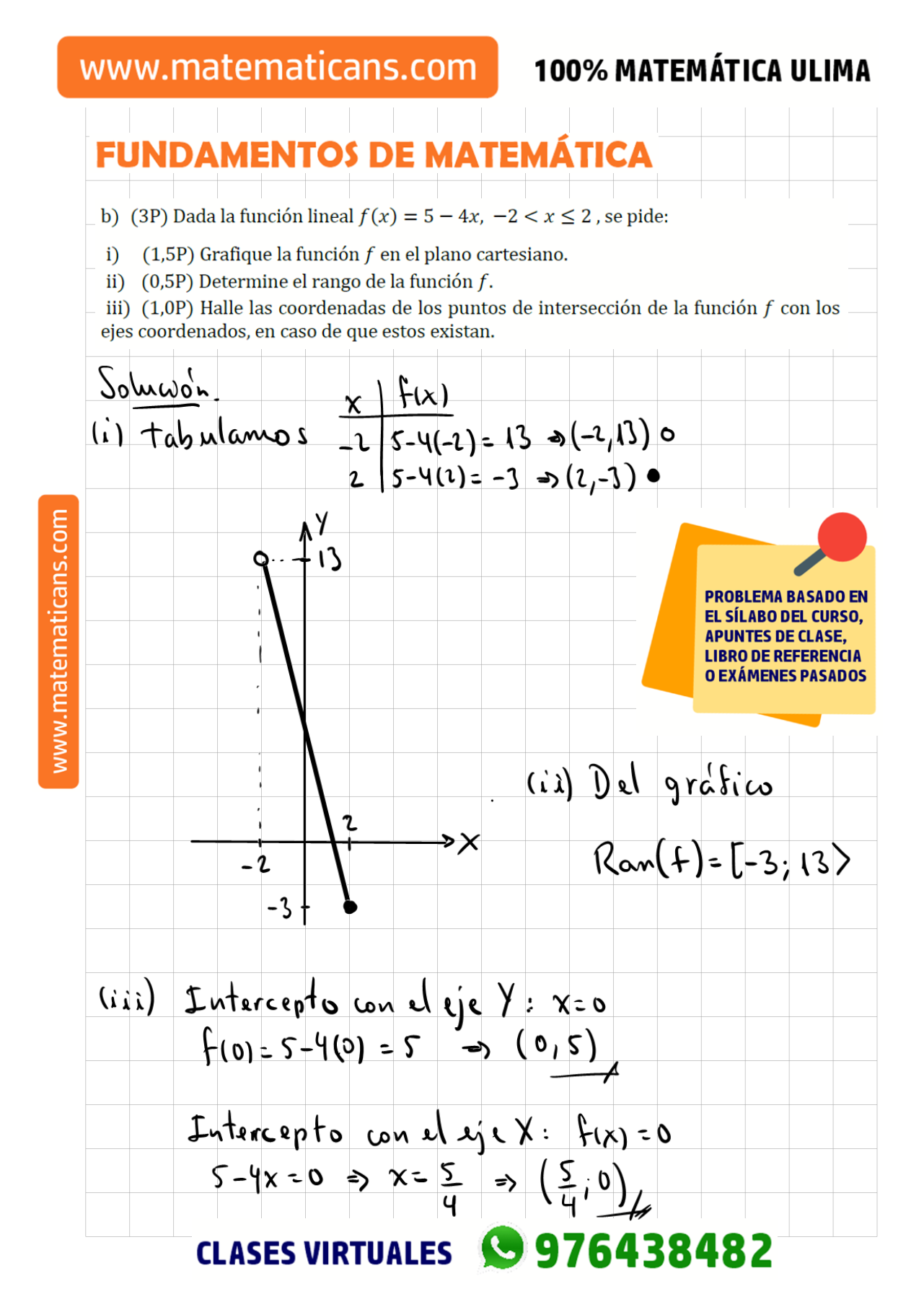
Pregunta de Examen de Fundamentos de Matemática ULIMA
Enunciado del problema (6 puntos)
En la siguiente tabla de distribución de frecuencias se muestran las estaturas en centímetros de 40 jóvenes candidatos a la selección de vóley masculino.
| Estatura (cm) | Número de estudiantes \(f_i\) |
|---|---|
| [ 158; 161 ⟩ | 2 |
| [ 161; 164 ⟩ | 12 |
| [ 164; 167 ⟩ | 8 |
| [ 167; 170 ⟩ | 4 |
| [ 170; 173 ⟩ | 10 |
| [ 173; 176 ] | 4 |
| Total | 40 |
En base a la información mostrada, se pide lo siguiente:
- (2 puntos) Elabore la tabla de distribución de frecuencias, acorde a la naturaleza de la variable, con el procedimiento adecuado que justifique sus respuestas.
- (2 puntos) Calcule e interprete \(f_2\) y \(H_5\), con el procedimiento adecuado que justifique sus respuestas.
- (2 puntos) Elabore un gráfico estadístico adecuado.
Teoría Necesaria
Para resolver este problema, necesitamos entender los conceptos básicos de una tabla de distribución de frecuencias para datos agrupados en intervalos.
- Variable Cuantitativa Continua: Es una variable que puede tomar cualquier valor dentro de un intervalo (ej. estatura, peso). Por eso se agrupan los datos.
- Intervalos de Clase: Rangos en los que se agrupan los datos. Se denotan como \([L_i; L_s\rangle\), donde \(L_i\) es el límite inferior (incluido) y \(L_s\) es el límite superior (no incluido, excepto a veces en el último intervalo).
- Frecuencia Absoluta (\(f_i\)): Número de datos que caen dentro de un intervalo de clase específico \(i\). La suma de todas las frecuencias absolutas es el número total de datos, \(n\). $$\sum f_i = n$$
- Frecuencia Absoluta Acumulada (\(F_i\)): Es la suma de las frecuencias absolutas desde el primer intervalo hasta el intervalo \(i\). Indica cuántos datos hay hasta el límite superior de ese intervalo. $$F_i = f_1 + f_2 + \dots + f_i$$
- Frecuencia Relativa (\(h_i\)): Es la proporción que representa la frecuencia absoluta de un intervalo respecto al total de datos. $$h_i = \frac{f_i}{n}$$
- Frecuencia Relativa Acumulada (\(H_i\)): Es la suma de las frecuencias relativas desde el primer intervalo hasta el intervalo \(i\). Indica la proporción de datos acumulados hasta ese punto. $$H_i = h_1 + h_2 + \dots + h_i$$ También se puede calcular como \(H_i = \frac{F_i}{n}\).
- Histograma: Es el gráfico estadístico más adecuado para representar variables cuantitativas continuas agrupadas en intervalos. Consiste en barras rectangulares adyacentes (sin espacios) cuya base es el intervalo de clase y su altura es proporcional a la frecuencia (absoluta o relativa).
Solución Detallada
a) Elaboración de la tabla de distribución de frecuencias
El problema nos da los intervalos y las frecuencias absolutas (\(f_i\)). El total de datos es \(n = 40\). Vamos a completar la tabla calculando las frecuencias absolutas acumuladas (\(F_i\)), las frecuencias relativas (\(h_i\)) y las frecuencias relativas acumuladas (\(H_i\)).
Cálculos paso a paso:
- Intervalo 1: [158; 161>
- \(f_1 = 2\)
- \(F_1 = f_1 = 2\)
- \(h_1 = \frac{f_1}{n} = \frac{2}{40} = 0.05\)
- \(H_1 = h_1 = 0.05\)
- Intervalo 2: [161; 164>
- \(f_2 = 12\)
- \(F_2 = F_1 + f_2 = 2 + 12 = 14\)
- \(h_2 = \frac{12}{40} = 0.30\)
- \(H_2 = H_1 + h_2 = 0.05 + 0.30 = 0.35\)
- Intervalo 3: [164; 167>
- \(f_3 = 8\)
- \(F_3 = F_2 + f_3 = 14 + 8 = 22\)
- \(h_3 = \frac{8}{40} = 0.20\)
- \(H_3 = H_2 + h_3 = 0.35 + 0.20 = 0.55\)
- Intervalo 4: [167; 170>
- \(f_4 = 4\)
- \(F_4 = F_3 + f_4 = 22 + 4 = 26\)
- \(h_4 = \frac{4}{40} = 0.10\)
- \(H_4 = H_3 + h_4 = 0.55 + 0.10 = 0.65\)
- Intervalo 5: [170; 173>
- \(f_5 = 10\)
- \(F_5 = F_4 + f_5 = 26 + 10 = 36\)
- \(h_5 = \frac{10}{40} = 0.25\)
- \(H_5 = H_4 + h_5 = 0.65 + 0.25 = 0.90\)
- Intervalo 6: [173; 176]
- \(f_6 = 4\)
- \(F_6 = F_5 + f_6 = 36 + 4 = 40\) (Debe coincidir con \(n\))
- \(h_6 = \frac{4}{40} = 0.10\)
- \(H_6 = H_5 + h_6 = 0.90 + 0.10 = 1.00\) (Debe ser 1)
Tabla de Frecuencias Completa:
| Estatura (cm) | Frecuencia Absoluta (\(f_i\)) | Frecuencia Absoluta Acumulada (\(F_i\)) | Frecuencia Relativa (\(h_i\)) | Frecuencia Relativa Acumulada (\(H_i\)) |
|---|---|---|---|---|
| [158; 161> | 2 | 2 | 0.05 | 0.05 |
| [161; 164> | 12 | 14 | 0.30 | 0.35 |
| [164; 167> | 8 | 22 | 0.20 | 0.55 |
| [167; 170> | 4 | 26 | 0.10 | 0.65 |
| [170; 173> | 10 | 36 | 0.25 | 0.90 |
| [173; 176] | 4 | 40 | 0.10 | 1.00 |
| Total | 40 | 1.00 |
b) Cálculo e interpretación de \(f_2\) y \(H_5\)
Cálculo e interpretación de \(f_2\):
Cálculo: Observando la tabla, la frecuencia absoluta del segundo intervalo (\(i=2\)) es \(f_2 = 12\).
Interpretación: La frecuencia absoluta indica la cantidad de estudiantes en ese rango de estatura. El segundo intervalo es [161; 164> cm. Por lo tanto, hay 12 estudiantes cuya estatura es mayor o igual a 161 cm y menor a 164 cm.
Cálculo e interpretación de \(H_5\):
Cálculo: \(H_5\) es la frecuencia relativa acumulada hasta el quinto intervalo. De nuestra tabla completa, vemos que \(H_5 = 0.90\).
Alternativamente, se calcula como:
\(H_5 = \frac{F_5}{n} = \frac{2+12+8+4+10}{40} = \frac{36}{40} = 0.90\).
Interpretación: La frecuencia relativa acumulada representa la proporción de estudiantes cuya estatura está por debajo del límite superior del intervalo en cuestión. El quinto intervalo es [170; 173>, y su límite superior es 173 cm. Esto significa que el 90% de los estudiantes (o una proporción de 0.90) tienen una estatura inferior a 173 cm.
c) Gráfico estadístico adecuado
Justificación: La variable de estudio es «Estatura», que es una variable cuantitativa continua. Además, los datos están presentados en una tabla de distribución de frecuencias con datos agrupados en intervalos de clase. Para este tipo de datos, el gráfico más adecuado es el histograma.
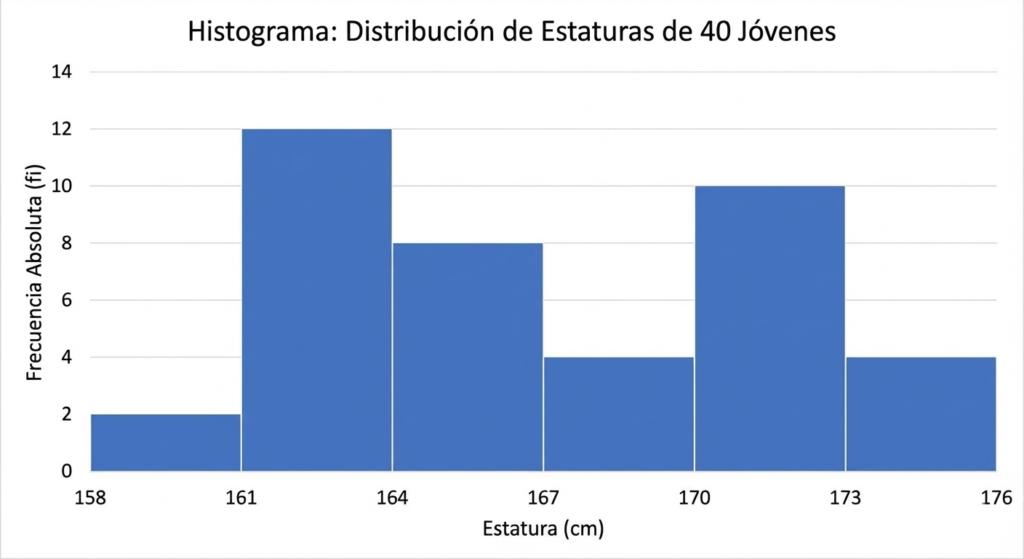
Descripción del Histograma:
- Eje Horizontal (X): Se representan los límites de los intervalos de estatura (158, 161, 164, 167, 170, 173, 176 cm).
- Eje Vertical (Y): Se representa la frecuencia absoluta (\(f_i\)) o la frecuencia relativa (\(h_i\)). En este caso, usaremos la frecuencia absoluta.
- Barras: Se dibujan barras rectangulares sobre cada intervalo. La anchura de la barra es el ancho del intervalo (3 cm) y su altura es igual a la frecuencia absoluta del intervalo.
- Una barra de altura 2 entre 158 y 161.
- Una barra de altura 12 entre 161 y 164.
- Una barra de altura 8 entre 164 y 167.
- Una barra de altura 4 entre 167 y 170.
- Una barra de altura 10 entre 170 y 173.
- Una barra de altura 4 entre 173 y 176.
- Importante: Las barras deben estar pegadas unas a otras, sin dejar espacios intermedios, para reflejar la naturaleza continua de la variable estatura.
Errores Comunes
- Confundir \(f_i\) con \(F_i\) (o \(h_i\) con \(H_i\)): Es vital diferenciar entre la frecuencia de un intervalo específico (absoluta o relativa) y la frecuencia acumulada hasta ese intervalo.
- Mala interpretación de las frecuencias acumuladas: Un error frecuente es pensar que \(H_i\) o \(F_i\) se refieren solo a los datos dentro del intervalo \(i\), cuando en realidad se refieren a todos los datos desde el principio hasta el final del intervalo \(i\). Por ejemplo, interpretar \(H_5 = 0.90\) como «el 90% de los estudiantes están entre 170 y 173 cm» es incorrecto; lo correcto es «el 90% miden menos de 173 cm».
- Usar un gráfico de barras con espacios: Para variables continuas, las barras deben estar juntas (histograma). Usar espacios sugiere incorrectamente que la variable es discreta o cualitativa.
- Errores de cálculo: Siempre verifica que la última frecuencia absoluta acumulada (\(F_k\)) sea igual al total de datos (\(n\)) y que la última frecuencia relativa acumulada (\(H_k\)) sea igual a 1.00.